Solving Sparse, Symmetric, Diagonally-Dominant
Linear Systems in Time O (m^{1.31})
Authors:
Daniel A. Spielman
and
Shang-Hua Teng
Bibliographic Information:
To appear in the Proceedings of the 44th Annual IEEE Symposium on Foundations of Computer Science.
Abstract
We present a linear-system solver that,
given an 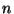 -by-
-by-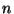 symmetric positive semi-definite, diagonally dominant
matrix
symmetric positive semi-definite, diagonally dominant
matrix 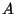 with
with 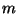 non-zero entries and an
non-zero entries and an 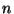 -vector
-vector 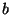 ,
produces a vector
,
produces a vector 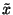 within relative distance
within relative distance 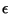 of the solution to
of the solution to 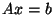 in time
in time
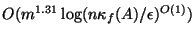 ,
where
,
where
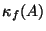 is the log of the ratio of the largest to smallest non-zero
eigenvalue of
is the log of the ratio of the largest to smallest non-zero
eigenvalue of 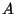 .
In particular,
.
In particular,
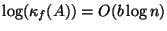 , where
, where
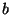 is the logarithm of the ratio of the largest to smallest
non-zero entry of
is the logarithm of the ratio of the largest to smallest
non-zero entry of 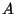 .
If the graph of
.
If the graph of 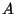 has genus
has genus 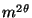 or does not have a
or does not have a
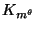 minor,
then the exponent of
minor,
then the exponent of 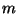 can be improved to
the minimum of
can be improved to
the minimum of
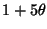 and
and
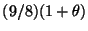 .
The key contribution of our work is an extension
of Vaidya's techniques for constructing and
analyzing combinatorial preconditioners.
.
The key contribution of our work is an extension
of Vaidya's techniques for constructing and
analyzing combinatorial preconditioners.
You can download the current version of the paper in
Postscript or
PDF.
This version includes proofs that were omitted from the FOCS version,
and cleans up some numerical details.
You can also download the FOCS version in
Postscript or
PDF.
Daniel A. Spielman
Last modified: Wed Mar 31 17:36:01 EST 2004